1 双气圈的动力学模型与求解
图1为双气圈的示意图。图l中,P为钢丝圈,Q为导纱钩,S点位于气圈环的中心平面位置。A、B分别为气圈Ⅱ(上气圈)和气圈Ⅱ(下气圈)在环面上的端点。以锭子的回转轴为z轴建立柱面坐标系,z轴的正方向朝上,原点位于钢丝圈所处的水平面上。纱线随钢丝圈以上的角速度旋转的同时,纱线以vs的线速度被卷取。
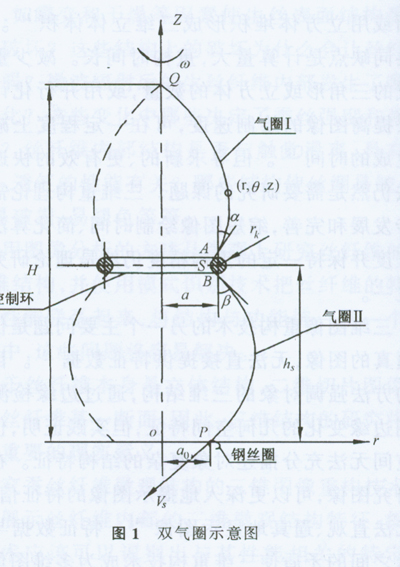
经动力学分析,得到Q点到P点的纱线应满足以下方程组:
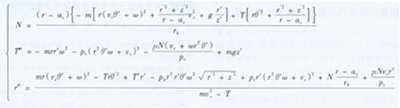
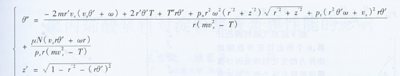
式中,m为纱线的线密度,N为正压力,T为纱线张力,W为气圈旋转角速度,Vs为卷绕线速度,Pn、Pt分别为法向空气阻力系数和切向空气阻力系数,u为摩擦系数,g为重力加速度,为对微元纱段ds求微分,Pc为中间变量。其它物理量如图1所示。
由式1可求解气圈环面上纱线的张力,当正压力N=0时,式(1)即为气圈上I ,Ⅱ的动力学表达方程式。
如图1所示,以s点为起点,沿纱线向上作数值计算,把θs和Ts作为未知初始变量,则有:

首先,任意设定θs,和Ts用数值法求解多元高阶微分方程(1),同时给定2个约束条件,即纱线从气圈环面上脱开角度a为某一数值以及当z=H时,rQ=0。计算时,反复调整未知初值θs和Ts,直到满足约束条件为止。然后,使用已确定的S点的初值求解气圈Ⅱ,以rp=ao。为约束条件,用数值法沿纱线向下求解方程(1),可解得包容角β,这样,整个双气圈的形态及张力即可求得。
2 双气圈的形态与张力
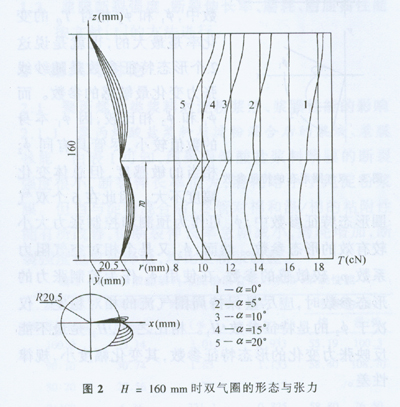
依据上述的动力学模型以及计算方法,本文对气圈高度H为150-230 mm的双气圈(其它物理量见表1)作了9组实例计算。图2为H=160 mm的双气圈形态与张力的计算结果。
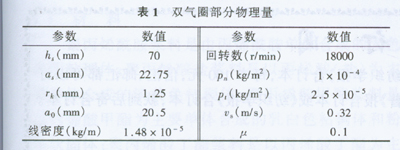
表1 双气圈部分物理量
由此可见,整个双气圈的形态及其张力,均与气圈环面上的纱线脱开角度α呈一一对应关系。当气圈高度为一定时,由a角的大小引起的双气圈形态的变化,影响到导纱钩处的纺出张力Tq。一般来说,TQ的大小变化由双气圈的形态特征决定。控制双气圈的形态特征值是控制张力保持恒定的有效途径。其中哪个特征参数对双气圈张力的变化最为敏感,则是本文需要探讨的另一个问题。
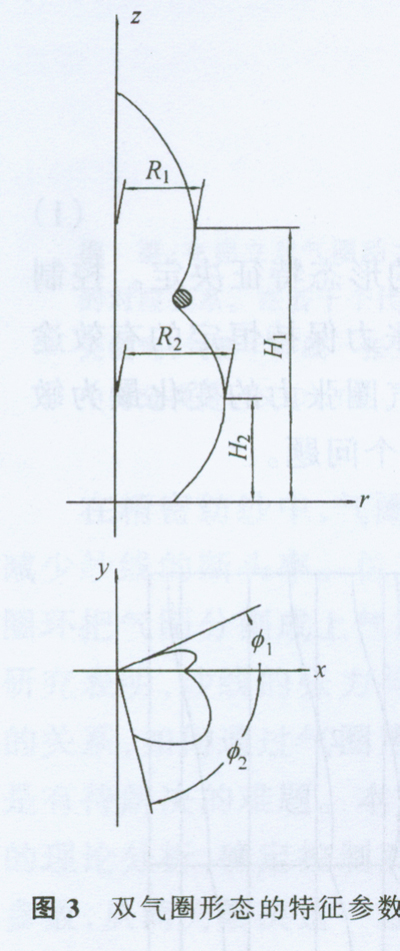
3 双气圈形态的特征参数
如图3中用6个参数来描述双气圈曲线,即气圈工的最大膨胀半径R1,最膨胀处的垂直高度H1,水平扭曲角度Ф1和气圈Ⅱ的最大膨胀半径R2,最膨胀处的垂直高度H2以及水平扭曲角度Ф2。
在气圈高度相同的情况下,不同的纺出张力了TQ对应着6组不同形态特征参数。本文通过对9条不同高度的双气圈的计算和分析,发现6个形态特征参数相对Tq的变化规律极其相似。在这里,列举2个例子,即H=160 mm和H=210 mm时双气圈形态特征参数与张力TQ的关系图表。为了便于比较,本文把6个形态特征参数作无量纲化处理,分别用以下来表示。
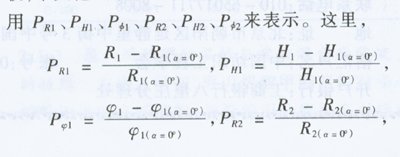

这里, 经9组双气圈的理论计算,6个形态特征参数随纺出张力的变化规律虽因计算精度所限有极个别不够连贯的点出现,但总体规律极为相似。张力小,则R1值大,H1值大,ф1值大,R2值大,H2值小,ф2值大,由图4可以看出,在6个形态特征参数中,ф1和ф2相对Tq的变化率是最大的,也就是说这2个形态特征参数是随纱线张力变化最敏感的参数。而ф1和ф2相比较,因声ф1本身的数值较小,尽管具有同声ф2相当的敏感度,但总体变化幅度不大。因此在6个双气圈形态特征参数中,ф2可作为预测和控制张力大小较有效的形态参数。然而,ф2又是个相对空气阻力系数Pn较敏感的参数,在使用ф2作为控制张力的形态参数时,应尽量保持周围气流的相对稳定。仅次于ф2的是特征参数Hl。相比之下,H2是最不能反映张力变化的形态特征参数,其变化幅度小,规律性差。

4 结 论
1.使用6个特征参数有效地描述了带控制环的双气圈的空间形态,并根据动力学模型得到形态特征参数与纺出张力的关系图表。
2.通过一系列的实例计算,分析得出下气圈的扭转角ф2为最能反映张力变化的形态特征参数。此结论为实现张力的实时控制提供了理论依据和可能性。