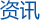纤维具有强力高、耐磨性、回弹性和尺寸稳定性好等优点。但它是一种典型的疏水性纤维,回潮率只有O.4%,因此其穿着舒适性很差,尤其当人体出汗时排汗困难,给人闷热不适的感觉。同时,因其吸湿性差,也给织造带来一系列问题,如易积聚静电、易吸灰尘,去除油污渍难等。
由于Coolbst纤维对水的接触角比较大,织物不易被润湿,因此对其进行亲水处理就显得很有必要,特别是用在导湿快干运动服装方面就更是如此。本文主要是利用PermaloseTM亲水剂对Coolbst纤维织物进行亲水处理,得出Perma—loseTM亲水剂对织物的导湿性能的影响,并得到最佳的亲水处理工艺及回归方程。
2实验材料及方法
2.1 实验材料
实验材料为3种由Coolbst短纤、长丝分别与棉、海岛丝交织的针织物,分别以代号k1,k2,k来表示,其织物参数及对应代号见表1。
2.2 实验仪器
本实验所用仪器为台湾Rapid染色(巨无霸型)试验机。
2.3 PermaloseTM亲水剂的亲水整理工艺
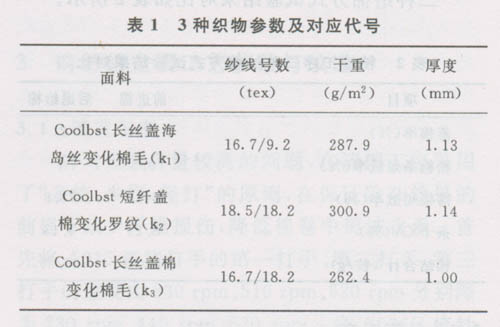
PermaloseTM亲水剂对3种织物的亲水处理工艺如下:
浸渍工艺:pH值:5;浴比:25:1;温度:80℃;时间:20 min。
PermaloseTM亲水剂用量(对织物重,即o•w•f,以下同):分别为2%~6%,间隔1%。
PermaloseTM亲水剂的亲水处理工艺曲线见图1。
2.4导湿性能测定
导湿实验:在织物反面滴一滴水,测取1min后织物正面的导湿面积s,这时可以测量在一定时间内,织物纵向的导湿高度a和横向的导湿宽度b,再按照椭圆面积公式计算导湿面积s:

3实验结果及分析
3.1织物k1的导湿性能
亲水剂用量与织物k1导湿面积的关系曲线如图2所示。
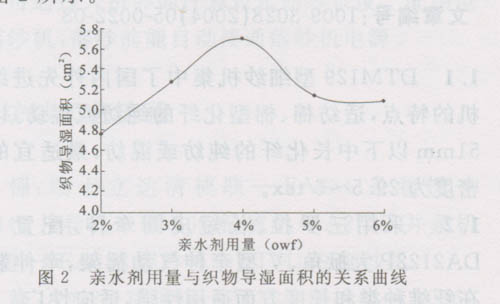
由图2可见,亲水剂用量为织物重量的2%~4%时,导湿面积随着亲水剂用量的增加而增加,在4%~6%时,随着亲水剂用量的增加,织物的导湿面积逐渐减小。在亲水剂用量为织物重量的4%时,导湿面积达到了一个最大值,亲水效果较好。由图2可知,考虑用抛物线进行回归,即要求确定的回归方程为:

此方程(2≤x≤6)的置信度为90.41%,当显著性水平大于0.0959时,回归模型成立。
3.2织物k2的导湿性能
亲水剂用量与织物k2导湿面积的关系曲线如图3所示。
由图3可以看出,随着亲水剂用量的逐渐增加,织物的导湿面积逐渐减小,当亲水剂用量为织物重量的4%时,导湿面积达到一个最小值,此后,随着亲水剂用量的逐渐增加,导湿面积逐渐增加。当亲水剂用量为织物重量的2%时织物的导湿面积最大。由图3亲水剂用量与导湿面积的关系曲线可知,考虑用抛物线进行回归,回归方程模型见公式(2),(3),经进行数学运算所得回归方程为:
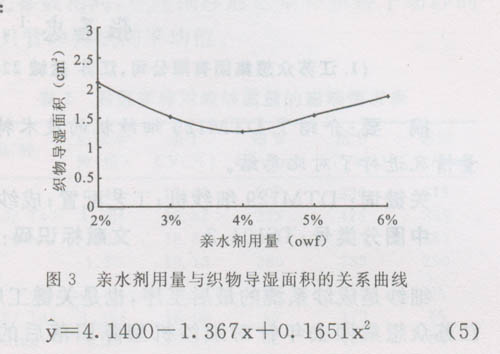
此方程(2≤x≤6)的置信度为95.99%,当显著性水平大于0.0401时,回归模型成立。
3.3织物k1的导湿性能
亲水剂用量与织物k3导湿面积的关系曲线如图4所示。

由图4可以看出,随着用量的逐渐增加,织物导湿面积逐渐减小,当亲水剂用量为织物重量的5%时,导湿面积达到最小值,此后,随着亲水剂用量的逐渐增加,织物的导湿面积逐渐增加。并且当亲水剂用量为织物重量的2%时,导湿面积是最大的。由图4亲水剂用量与导湿面积的关系曲线可知,考虑用抛物线进行回归,回归方程模型见公式(2),(3),经进行数学运算所得回归方程为:
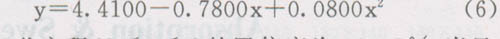
此方程(2≤x≤6)的置信度为91.07%,当显著性水平大于O.0893时,回归模型成立。
4 结论
通过用PermaloseTM亲水剂对三种Coolbst织物分别进行亲水整理,然后利用滴液法测量织物1 min导湿面积,得出以下结论:
4.1对织物k1,织物内外层原料分别为Coolbst长丝和海岛丝,经亲水处理后,导湿性能的变化规律为:开始随着亲水剂用量的增加,织物的导湿面积逐渐增大,当亲水剂用量达到一定值后,导湿面积达到最大值,此后,随着亲水剂用量的增加,导湿面积逐渐减小。
4.2 对织物k2及k1,织物内外层原料分别为Coolbst纤维和棉,经亲水处理后,导湿性能的变化规律为:开始随着亲水剂用量的增加,织物的导湿面积不但不增大反而减小,当亲水剂用量达到一定值后,导湿面积达到一个最小值,此后,随着亲水剂用量的增加,织物的导湿面积又逐渐增大。
4.3利用所得数据,对亲水剂用量与导湿面积的关系进行回归,回归方程都为抛物线,而且方程的置信度都大于90%。这就表明了回归方程与实验数据有很好的吻合性。